Regression linéaire avec R

la fonction lm permet de produire un tel modèle, d'estimer sa fiabilité et de l'illustrer graphiquement

Construction du modèle

> vv = read.table("Data/ventes_visites.txt")
> vv.lm = lm(data=vv, formula = ventes~visites)
> vv.lm

Call:
lm(formula = ventes ~ visites, data = vv)

Coefficients:
(Intercept)      visites  
    56.0429       0.7571

 ventes = 56.0429 + 0.7571 * visites

Validité du modèle

> summary(vv.lm)

Call:
lm(formula = ventes ~ visites, data = vv)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.00000 -0.85714 -0.04286  0.66429  2.48571 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  56.0429     3.7477  14.954 5.63e-06 ***
visites       0.7571     0.1279   5.919  0.00104 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.513 on 6 degrees of freedom
Multiple R-squared:  0.8538,	Adjusted R-squared:  0.8294 
F-statistic: 35.04 on 1 and 6 DF,  p-value: 0.001035

F : plus elle est grande, meilleur est le modèle
R² ajusté : plus il est proche de 1 meilleur est le modèle (au delà des 95%)
t : (correspond au coeffificient divisé par l'écart type), sa valeur absolue doit être supérieure à 2 pour que l'apport de la variable associée soit significatif.
Les degrés de libertés du modèle correspondent au nombre d'observations moins le nombre de coéfficient à estimer

Attributs de l'objet vv.lm

> vv.lm$
vv.lm$coefficients   vv.lm$rank           vv.lm$qr             vv.lm$call
vv.lm$residuals      vv.lm$fitted.values  vv.lm$df.residual    vv.lm$terms
vv.lm$effects        vv.lm$assign         vv.lm$xlevels        vv.lm$model

Valeurs à modéliser
```
> vv$ventes
[1] 75 76 82 82 76 83 76 74
```

Valeurs calculées par le modèle

vv.lm$fitted.values
       1        2        3        4        5        6        7        8
75.72857 77.24286 81.78571 79.51429 78.00000 83.30000 74.97143 73.45714

Erreurs commises sur chaque exemple

vv.lm$residuals
         1          2          3          4          5          6          7         8
-0.7285714 -1.2428571  0.2142857  2.4857143 -2.0000000 -0.3000000  1.0285714  0.5428571

La qualité du modèle mesuré par R² (coefficient de détermination) exprime le ratio entre la variance du modèle et la variance de la variable modélisée :

> var(vv.lm$fitted.values)
[1] 11.46531
> var(vv$ventes)
[1] 13.42857
> var(vv.lm$fitted.values)/var(vv$ventes)
[1] 0.8537994
> summary(vv.lm)$r.squared
[1] 0.8537994

La statistique F se calcule en fonction de R² (R²=0.8537994), du nombre de variables explicatives utilisées (p=1) et du nombre d'observations (n=8) : F=(R²/p)/((1-R²)/(n-p-1))
```
(0.8537994/1)/((1-0.8537994)/(8-1-1))
[1] 35.0395
```

Représentation graphique du modèle

> png("images/visu_lm.png")
> par(mfrow=c(2,2))
> plot(vv.lm)
> dev.off()

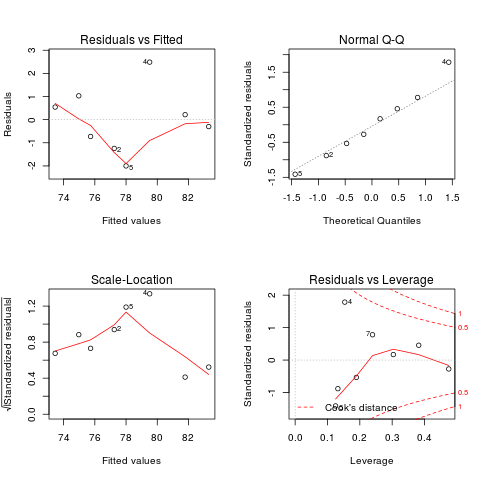
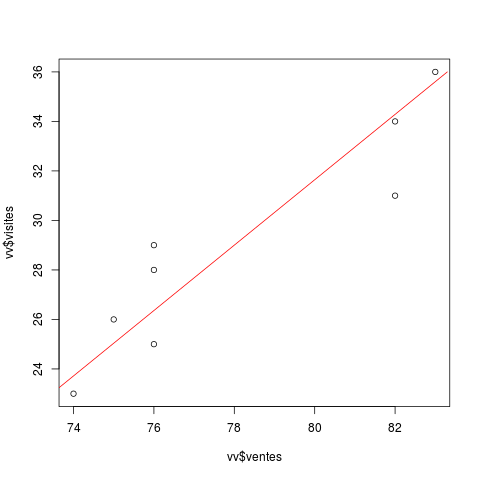
graphiques illustrants le résultat de la régression linéaire

Affichage des points et de la droite modélisée

> png("images/plot_vv.png")
> plot(vv$ventes, vv$visites)
> lines(56.0429+0.7571*vv$visites, vv$visites, col="red")
> dev.off()