<< Notions de base | PythonIndex | >>

Les fonctions

Plan (hide)

  1.   1.  Pour commencer
    1.   1.1  Les fonctions des matheux

1.  Pour commencer

Lorsque l'on écrit un programme on apprend à l'ordinateur comment réaliser de nouveaux traitements qu'il n'était pas en mesure d'effectuer auparavant. Ce programme est constitué d'instructions de base, celles que nous avons déjà vu comme les boucles ou les instructions conditionnelles, mais Ana tu peux ajouter des nouvelles instructions qui seront alors "comprises" par l'ordinateur. Ces nouvelles instructions se définissent à l'aide de fonctions, c'est ce que nous allons développer ici.

1.1  Les fonctions des matheux

Tu as déjà entendu parler de fonctions en mathématiques. En général, on définit un ensemble de départ {$ E $} et un ensemble d'arrivée {$ F $} et une relation de {$ E $} vers {$ F $}. Chaque élément de {$ E $} possède au plus une image dans {$ F $}. Par exemple {$$ f: \left\{ 

  \begin{array}{rcl}
    \mathbf{R} & \longrightarrow &\mathbf{R} 
    x & \longmapsto & 2x^2 + 1 
  \end{array}

\right. $$}

L'ensemble de départ ainsi que celui d'arrivée est {$ \mathbf{R} $}, l'ensemble des réels. À {$ x $} on associe {$ 2x^2 + 1 $}, ainsi par exemple à 2 on associe 9.

Cette fonction {$ f $} se traduit en python de la façon suivante :

#! /usr/bin/env python3
# -*- coding: utf-8 -*- Pour le plaisir des accents
def f(x):
    return 2*x**2 + 1
[$[Get Code]]

Tu peux la sauvegarder dans un fichier fonc1.py et demander son exécution sous idle3.

"Mais Conda, il ne se passe rien".

C'est normal, il faut maintenant appeler ta fonction au niveau du shell python. 

 >>> f(3)
 19
 >>> f(2)
 9
 >>>

Tu as vu return indique ce que l'on retourne.

On peut représenter cette fonction dans un repère orthonormé. Pour cela il nous faut avant installer matplolib. Ana si tu veux on le fera ensemble. Tu peux sauter ce qui suit et aller directement ici.

Linux

 % sudo add-apt-repository ppa:takluyver/matplotlib-daily

Ensuite, il suffit de modifier le fichier /etc/apt/sources.list 

 % sudo gedit /etc/apt/sources.list

en ajoutant à la fin les lignes suivantes : 

 # python3 matplotlib
 deb http://ppa.launchpad.net/takluyver/matplotlib-daily/ubuntu  precise main
 deb-src http://ppa.launchpad.net/takluyver/matplotlib-daily/ubuntu precise main

 deb http://ppa.launchpad.net/takluyver/python3/ubuntu precise main
 deb-src http://ppa.launchpad.net/takluyver/python3/ubuntu precise main

puis 

 % sudo apt-get update
 % sudo apt-get install ipython3 python3-numpy python3-scipy python3-sympy python3-matplotlib

Une autre solution consiste à utiliser pip.

Windows

Le plus simple est d'aller sur cette page et récupérer les éléments nécessaires.

La fonction f et son graphe

On a donc défini notre fonction f précédemment. On commence par générer un tableau de valeur pour x à l'aide de arange. Pour cela on donne la valeur initiale -10 et la valeur finale 10 et le pas de variation 0.01. La première valeur est donc -10.0, la seconde -10.0 + 0.01 donc -9.99 et ainsi de suite. 

 x = arange(-10.0, 10.0, 0.01)

"QUOI ! ?? "

Ok, ok je n'ai pas encore parlé de tableau, pour le moment considère que c'est plusieurs valeurs et il y en a une première, une deuxième, une troisième ....

On construit ensuite un tableau de valeur pour y avec y = f(x). et on trace.

#! /usr/bin/env python3
# -*- coding: utf-8 -*- Pour le plaisir des accents

from pylab import *

# La fonction dont on effectue le tracé
def f(x):
    return 2*x**2 + 1

# On génère un tableau de nombre pour x
# array([-10.  ,  -9.99,  -9.98, ...,   9.97,   9.98,   9.99])
x = arange(-10.0, 10.0, 0.01)
# On génère un tableau de nombre pour y
# array([ 201.    ,  200.6002,  200.2008, ...,  199.8018,  200.2008,
#        200.6002])
y = f(x)

# On trace l'ensemble de points
plot(x, y)
grid(True)
show()
[$[Get Code]]

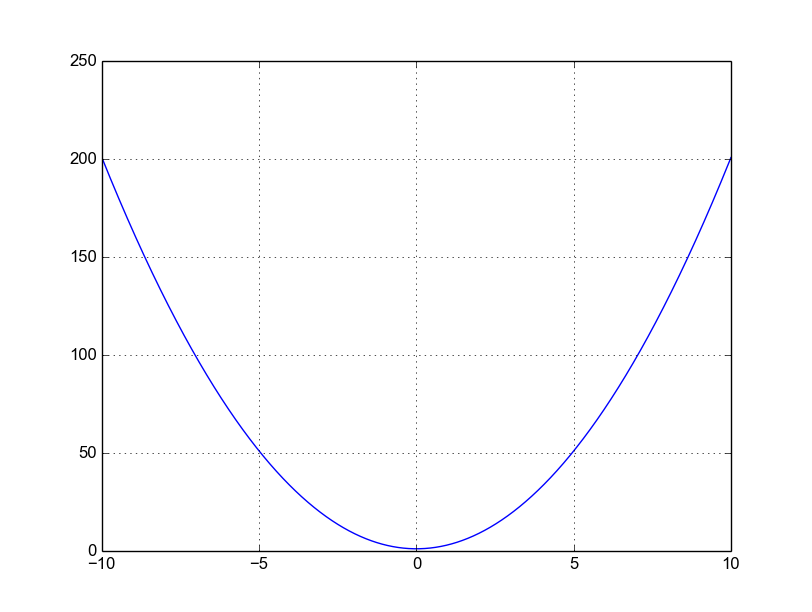
Ana tu peux constater que le fait d'avoir défini la fonction cela nous évite de réécrire à chaque fois le calcul, ce point est important. D'autre part, on peut remarquer que l'on transmet une information à la fonction f par exemple 2 lorsqu'on écrit f(2) et que celle-ci nous retourne un résultat 9 dans le cas présent (ce ne sera pas toujours le cas). Les fonctions nous permettent aussi de rendre le programme plus lisible, elles structurent le code.

Avant de regarder plus avant les fonctions en python je te propose de résumer ce que nous venons de voir :

  • on donne un nom à la fonction ;
  • on définit une liste de paramètres ;
  • on associe un traitement (algorithme) sous la forme d'instruction ;
  • on retourne éventuellement un résultat.

Notre fonction f avait un unique paramètre x et retournait 2*x**2 + 1. D'une façon générale un fonction va donc s'écrire de la façon suivante :

def nom_de_la_fonction(liste_de_paramètres):

bloc d'intructions
return valeur