<< Installation de Python | PythonIndex | Notions de base >>
Exemple d'utilisation
Plan (hide)
1. Quelques explications

Tablette du calcul de {$\sqrt(2)$} source
Ana cette page vient sans doute un peu tôt car elle fait appel à des notions que je n'ai pas encore présentées. Elle a juste pour objectif de te montrer l'utilité de python pour réaliser des traitements ou des calculs qui peuvent s'avérer utiles en mathématiques, en physiques ou en sciences naturelles, par exemple.
2. Valeur approchée de {$\sqrt(2)$}
Il y a environ 4000 ans les Babyloniens avait déjà déterminé une approximation de {$\sqrt(2)$} en utilisant une suite finie d'opérations et d'instructions, un algorithme. La valeur qu'ils avaient trouvée était en sexagésimal {$(1,oPa)_{60} = 1 + 24/60 + 51/3600 + 10/216000 = 1.41421296$}. Pas mal !
Comment ont ils procédé ? Ce n'est qu'une hypothèse car on n'a pas retrouvé de trace concernant la méthode. Pour extraire la racine carré d'un nombre {$x$}, cela revient à résoudre l'équation {$x^2 = A$}, pour cela il suffit de déterminer un carré dont l'aire est {$A$}. Ana considère donc un rectangle dont la longueur d'un des cotés est {$a_0$}, l'autre coté pour que la surface soit de {$A$} est de longueur {$A/a_0$}, il y a malheureusement peu de chance que cela soit égal à {$a_0$}. On va donc essayer de rendre le rectangle un peu plus carré, pour cela on prend la moyenne arithmétique de la longueur de nos deux cotés : {$$ a_1 = \frac{a_0 + \frac{A}{a_0}}{2} $$}
On recommence jusqu'à ce que notre rectangle soit carré. On dit souvent que l'on itère et une itération se transformera dans nos programme en boucle. {$$ a_i = \frac{a_{i-1} + \frac{A}{a_{i-1}}}{2} $$}
On va l'écrire en python
# -*- coding: utf-8 -*-
A = 2.
a = 1.
old_a = 0
precision = 1E-8
while(abs(a - old_a) > precision):
old_a = a
a = (a + A/a)/2
print(old_a, a)
En utilisant mathplotlibb, Ana tu peux suivre la correspondance géométrique. Je te propose de réécrire un peu le programme afin de mieux le structurer et de le généraliser.
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import matplotlib.patches as patches
def sqrtHeron(aire, precision):
a = 1.
old_a = 0
liste = [(a, aire/a)]
while(abs(a - old_a) > precision):
old_a = a
a = (a + aire/a)/2
liste.append((a, aire/a))
dessineRectangle(liste, aire)
return a
def dessineRectangle(liste, borne):
figure = plt.figure()
axe = figure.add_subplot(111)
axe.set_xlim([0, borne])
axe.set_ylim([0, borne])
epaisseur = 0;
for elt in liste :
epaisseur = epaisseur + 0.1
axe.add_patch(
patches.Rectangle(
(0, 0), # (x,y)
elt[0], # width
elt[1], # height
fill = False,
linewidth=epaisseur
)
)
plt.show()
def main():
x = float(input('Entrez la valeur dont vous voulez extraire la racine : '))
print('sqrt({}) = {}'.format(x, sqrtHeron(x, 1E-8)))
main()
Voila ce que cela donne :
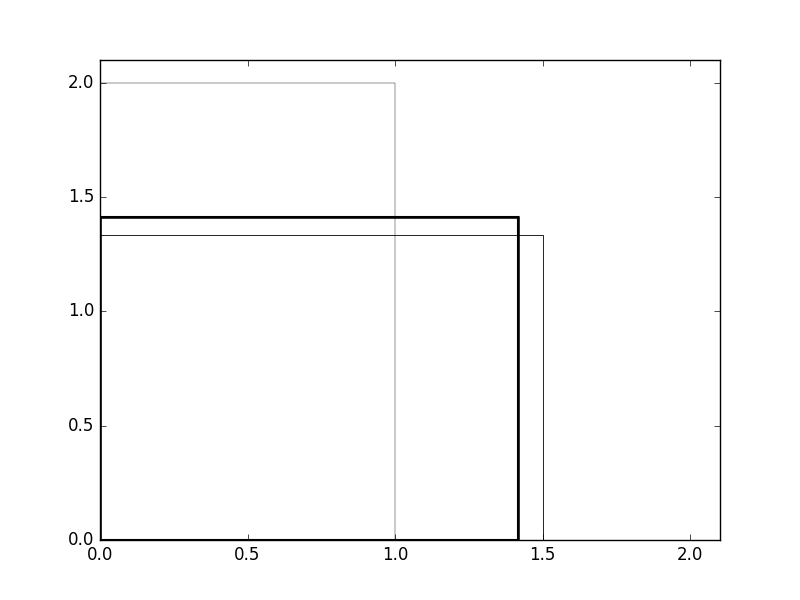
3. Convergence
La suite des valeurs calculées semble converger vers {$\sqrt(2)$}, cela est-il bien vrai ? Généralisons notre propos en considérant la suite {$a_n$}.
{$\left\{\begin{array}{rcl}
a_0 &>& \sqrt{A}\\a_n &=& \frac{a_{n-1} + \frac{A}{a_{n-1}}}{2},\forall n \in \mathbb{N}^*
\end{array}
\right.$}
- Proposition
- La suite {$a_n$} est minorée par {$\sqrt{A}$}
- Démonstration
- Commençons par montrer que :
{$ \forall x \in \mathbb{R}^*, f(x) = \frac{x + \frac{A}{x}}{2} \ge \sqrt{A} $}
Considérons :
{$ x + \frac{A}{2} \ge 2 \sqrt{A}, ~~~~~x - 2 \sqrt{A} + \frac{A}{2} \ge 0, ~~~~~(\sqrt{x} - \sqrt{\frac{A}{2}})^2 \ge 0 $}
Un carré étant toujours positif, cette dernière inégalité est vraie.
Par récurrence maintenant :
- Le premier terme de la suite {$a_0$} est bien strictement supérieur {$\sqrt{A}$}.
- Supposons que pour {$n > 0$} on ait


