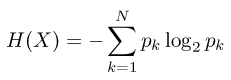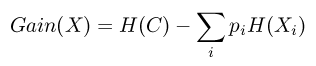Entropie croisée

Issue de la théorie de l'information (Shannon)
Mesure l'homogénéité entre deux distributions de probabilités
L'entropie d'une variable aléatoire est définie par :
On estime la probabilité d'une modalité par son ratio (poids) dans l'échantillon traité
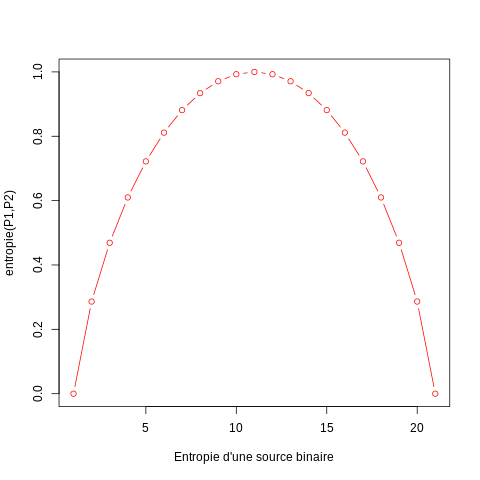
Exemple avec la séquence de répartition des probabilités suivante :

P₁ 0.00 0.05 0.10 ... 0.95 1.00

P₂ 1.00 0.95 0.90 ... 0.05 0.00

On peut observer l'évolution de la courbe de la fonction d'entropie
Le gain d'information apporté par une variable est alors représenté par la différence entre l'entropie de cette variable et l'entropie de cette même variable conditionnée par la classe
La meilleure partition correspond à la variable qui maximise ce gain d'information

P₁	0.00	0.05	0.10	...	0.95	1.00
P₂	1.00	0.95	0.90	...	0.05	0.00