Docs
CM
ACP
Procédez à l'étude des données associées aux fichiers suivants : exoReg1.txt.
> reg1=read.table("exoReg1.txt")
> acp = princomp(reg1,cor=TRUE)
> acp
Call:
princomp(x = reg1, cor = TRUE)
Standard deviations:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
1.79207900 1.25543181 0.44595569 0.10893290 0.04001203
5 variables and 13 observations.
> summary(acp)
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
Standard deviation 1.7920790 1.2554318 0.44595569 0.108932897 0.0400120302
Proportion of Variance 0.6423094 0.3152218 0.03977530 0.002373275 0.0003201925
Cumulative Proportion 0.6423094 0.9575312 0.99730653 0.999679807 1.0000000000
> par(mfrow=c(1,2))
> plot (acp)
> biplot(acp)
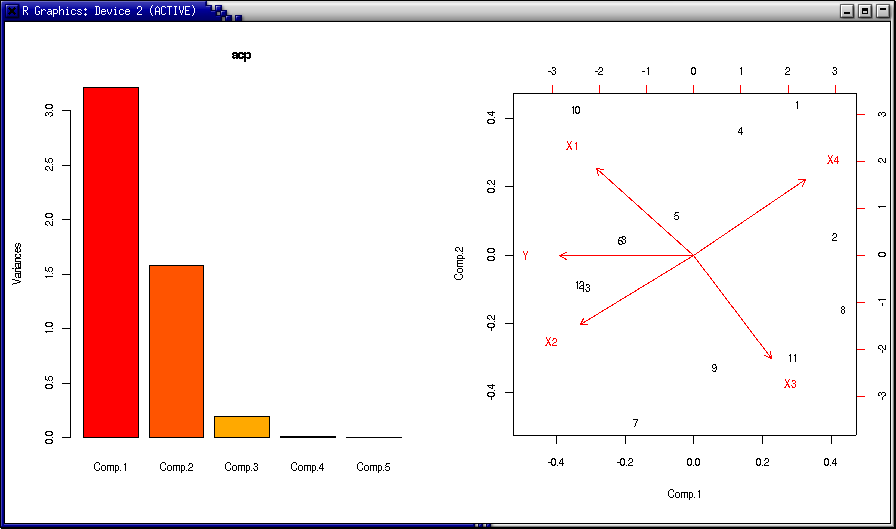
> acp$sdev
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
1.79207900 1.25543181 0.44595569 0.10893290 0.04001203
> acp$sdev*acp$sdev
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
3.211547154 1.576109031 0.198876476 0.011866376 0.001600963
> eigen(cor(reg1))
$values
[1] 3.211547154 1.576109031 0.198876476 0.011866376 0.001600963
$vectors
[,1] [,2] [,3] [,4] [,5]
[1,] 0.5533800 -0.003342949 0.2106032 0.80495783 -0.0380602
[2,] 0.4011658 0.512413468 0.5812090 -0.41341229 0.2603552
[3,] 0.4682512 -0.409678782 -0.3896683 -0.19084641 0.6516444
[4,] -0.3189779 -0.607968833 0.6746443 0.05282357 0.2658790
[5,] -0.4602504 0.447167145 -0.1041923 0.37672337 0.6598747
> acp$loadings
Loadings:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
Y -0.553 0.211 0.805
X1 -0.401 0.512 0.581 -0.413 0.260
X2 -0.468 -0.410 -0.390 -0.191 0.652
X3 0.319 -0.608 0.675 0.266
X4 0.460 0.447 -0.104 0.377 0.660
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
SS loadings 1.0 1.0 1.0 1.0 1.0
Proportion Var 0.2 0.2 0.2 0.2 0.2
Cumulative Var 0.2 0.4 0.6 0.8 1.0
> acp$center
Y X1 X2 X3 X4
95.438462 7.461538 48.153846 11.769231 30.000000
> acp$scale
Y X1 X2 X3 X4
14.431138 5.651622 14.950411 6.153846 16.081523
> acp$n.obs
[1] 13
> acp$scores
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
1 1.9357055 1.9733074 -0.54408887 0.025000659 0.03952149
2 2.6585707 0.2364222 -0.25919227 0.092331415 -0.03498866
3 -1.3182914 0.1980815 -0.05971679 -0.131317652 -0.09155472
4 0.8778336 1.6377820 0.17323706 -0.111200481 -0.02929345
5 -0.3185821 0.5060423 -0.79289121 0.031163656 0.01900113
6 -1.3657941 0.1811666 0.13452792 0.210201419 -0.02279333
7 -1.0930548 -2.2163607 -0.21936861 -0.077556747 0.01231682
8 2.8065014 -0.7319342 0.47873229 -0.172077644 0.03163279
9 0.3882477 -1.4928554 -0.01325269 0.060519403 -0.04967684
10 -2.2266661 1.9107006 0.89514664 0.005335703 0.01961902
11 1.8569418 -1.3580321 0.58348404 0.117665351 0.02698841
12 -2.1537352 -0.3992735 -0.02755253 0.064219514 0.03552010
13 -2.0476770 -0.4450468 -0.34906497 -0.114284596 0.04370725
- acp$sdev :
- les écarts-types correspondent à la racine carré des valeurs propres
- proportion of variance :
- exprimée par les valeurs propres (eigen values en anglais)
- acp$loading :
- Matrice de rotation simplifiée, obtenue avec les vecteurs propres
- acp$center :
- centres associés à la matrice de rotation utilisée pour changer de repère
- acp$scale :
- echelle
- acp$scores
- Coordonnées des exemples dans le nouveau repère
Exercice
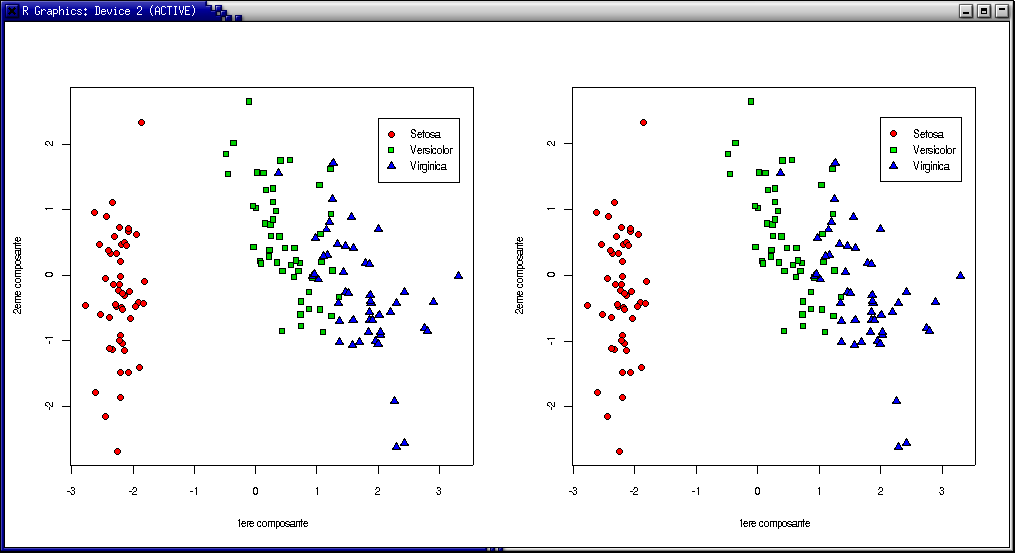
Réaliser une ACP sur les données iris et comparer les projections obtenues avec les deux méthodes sur les données iris :
> data(iris)
> irisACP = princomp(iris[1:4],cor=TRUE)
> irisACP2 = prcomp(iris[1:4],scale=TRUE)
> par(mfrow=c(1,2))
> plot(irisACP$scores[,1],irisACP$scores[,2],pch=c(rep(21,times=50),rep(22,times=50),rep(24,times=50)),
bg=c("red", "green3", "blue")[unclass(iris$Species)],xlab="1ere composante",ylab="2eme composante")
> legend(2.,2.4,c("Setosa","Versicolor","Virginica"),pch=c(21,22,24),pt.bg=c("red","green","blue"))
> plot(irisACP2$x[,1],irisACP2$x[,2],pch=c(rep(21,times=50),rep(22,times=50),rep(24,times=50)),
bg=c("red", "green3", "blue")[unclass(iris$Species)],xlab="1ere composante",ylab="2eme composante")
> legend(2.,2.4,c("Setosa","Versicolor","Virginica"),pch=c(21,22,24),pt.bg=c("red","green","blue"))