home	accès étudiants

Branch and bound parallèle

Le compte rendu du TP contiendra :

un rapport en format PDF
les fichiers contenant le code source
un Makefile
un fichier README contenant instructions d'exécution

Décrivez les algorithmes en pseudo-langage. Dans l'algorithme ne faites apparaître que les idées essentielles, il ne s'agit pas de retranscrire la gestion des pointeurs. Indiquez par contre comment sont gérées les données (partionnement, répartition, envois et reception). Le TP est à rendre par e-mail à [stefan dot balev at univ dash lehavre dot fr].

Le problème du sac à dos

Nous avons n objets. Le coût de l'objet i est c_i et son poids est a_i. Le problème du sac à dos consiste à choisir un sous-ensemble d'objets de coût total maximum et de poids ne dépassant pas la capacité du sac à dos, b. On suppose que c_i, a_i et b sont des entiers positifs. On suppose aussi que pour chaque i, a_i ≤ b (sinon on peut éliminer l'objet i) et que a₁ + ... + a_n > b (sinon on peut prendre tous les objets).

En introduisant des variables binaires x_i qui prennent la valeur 1 si l'objet i est choisi et 0 sinon, on peut donner la formulation suivante:

z = max c₁ x₁ + ... + c_n x_n
    sous contraintes :
        a₁ x₁ + ... + a_n x_n ≤ b
        x_i = 0 ou 1, i = 1,...,n

Le nombre de sous-ensembles d'objets est 2ⁿ et donc pour des problèmes de grande taille il est impossible de trouver la meilleure solution en explorant toutes les possibilités, même en utilisant une machine parallèle puissante.

Algorithme branch and bound

La méthode par séparation et évaluation (branch and bound) s'applique à la résolution de problèmes d'optimisation combinatoire avec un grand nombre de solutions envisageables. Il consiste à séparer le problème initial en plusieurs sous-problèmes et d'éliminer certains sous-problèmes à l'aide d'un système de majorants et minorants.

Nous allons montrer le fonctionnement de cette méthode sur l'exemple suivant:

z = max  8 x1 + 16 x2 + 20 x3 + 12 x4 +  6 x5 +  9 x6 +  2 x7
         3 x1 +  7 x2 +  9 x3 +  6 x4 +  3 x5 +  5 x6 +  2 x7 ≤ 17
	 x1,...,x7 = 0 ou 1

D'abord on va trier les objets en ordre décroissant du rapport coût / poids. Dans notre exemple, nous avons

8/3 ≥ 16/7 ≥ 20/9 ≥ 12/6 ≥ 6/3 ≥ 9/5 ≥ 2/2

et les objets sont déjà triés.

Recherche de solution initiale

On va utiliser une approche glouton. En commençant par le premier objet, on met des objets dans le sac à dos tant que la capacité le permet. Dans notre exemple on choisit les objets 1 et 2. La capacité restante 7 ne permet pas de choisir l'objet 3. En rajoutant l'objet 4 il nous reste capacité 1 et les objets 5, 6 et 7 ne peuvent pas entrer dans le sac à dos. Ainsi, on obtient la solution

x = (1 1 0 1 0 0 0)

de coût z^* = 8 + 16 + 12 = 36. C'est la meilleure solution réalisable jusqu'au maintenant. On va appeler z^* le record.

Evaluation

Pour chaque sous-problème nous allons calculer un majorant sur le coût. Pour calculer le majorant, nous allons remplacer les contraintes d'intégrité

x_i = 0 ou 1

par les contraintes plus faibles

0 ≤ x_i ≤ 1

Ainsi on obtient un problème plus facile à résoudre que le problème initial qu'on appelle relaxation. Pour résoudre cette relaxation il nous suffit de prendre les objets dans l'ordre tant que la capacité nous le permet. Pour notre exemple on prend les objets 1 et 2 et il nous reste 7 unités de capacité. C'est pourquoi on prend 7/9 de l'objet 3. Cela nous donne la solution

x = (1 1 7/9 0 0 0 0)

et le majorant 8 + 16 + 20 * 7 / 9 = 39 5/9. Sachant que les coûts sont tous entiers, on peut prendre la partie entière u = 39 comme majorant. Maintenant on sait que le coût de la meilleure solution est entre 36 et 39.

Si le majorant ainsi calculé est inférieur ou égal au record courant (le meilleur minorant connu), on peut éliminer le sous-problème.

Si dans la solution de la relaxation toutes les variables sont entières, il s'agit d'une solution réalisable du problème non relaxé. Si en plus la valeur de cette solution est supérieure au record courant, il s'agit d'un nouveau record.

Séparation

Si on se retrouve avec un majorant supérieur au record et une solution avec une variable non entière, on sépare le problème traité en deux sous-problèmes en fixant la variable à 0 et à 1. Dans notre exemple nous avons:

z =  0 + max  8 x1 + 16 x2 + 12 x4 +  6 x5 +  9 x6 +  2 x7
              3 x1 +  7 x2 +  6 x4 +  3 x5 +  5 x6 +  2 x7 ≤ 17

z = 20 + max  8 x1 + 16 x2 + 12 x4 +  6 x5 +  9 x6 +  2 x7
              3 x1 +  7 x2 +  6 x4 +  3 x5 +  5 x6 +  2 x7 ≤ 8

On traite chaque sous-problème de la même manière.

En résume

Trier les objets en ordre décroissant du rapport c_i / a_i
Trouver une solution initiale x* en utilisant l'algorithme glouton.
z* = c x*
Mettre le problème initial dans un pool de sous-problèmes
tant que le pool n'est pas vide
{  choisir un sous-problème P du pool
   trouver la solution x de la relaxation et le majorant u = c x
   si u <= z*
   {  // rien à faire, on élimine le sous-problème
   }
   sinon si x est entier
   {  // nouveau record trouvé
      z* = u
      x* = x
   }
   sinon
   {  // séparation
      soit x_i la variable non entière
      créer un sous-problème P0 en fixant x_i à 0
      créer un sous-problème P1 en fixant x_i à 1
      mettre P0 et P1 dans le pool
   }
}
afficher la solution optimale x*

Exemple

L'arbre suivant donne le déroulement de l'algorithme branch and bound pour notre exemple. Chaque noeud représente un sous-problème. On donne l'ordre de traitement des sous-problèmes, la borne supérieure et la variable non entière.

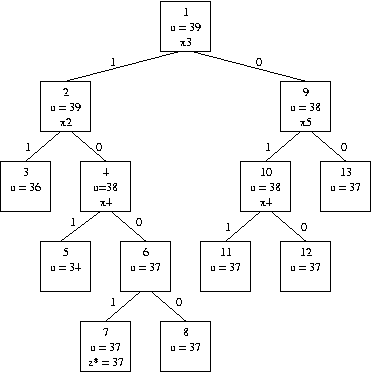
Ensuite on donne chaque sous-problème et la solution de sa relaxation. A noter que lorsqu'on fixe une variable à 1, on diminue la capacité du sac à dos b et on peut fixer à zéro toutes les variables x_i pour lesquelles a_i ≥ b (cf sous-problèmes 3 et 5)

 1:  0 + max  8 x1 + 16 x2 + 20 x3 + 12 x4 +  6 x5 +  9 x6 +  2 x7
              3 x1 +  7 x2 +  9 x3 +  6 x4 +  3 x5 +  5 x6 +  2 x7 ≤ 17
    sol:        1       1       7/9     0       0       0       0
    ub = 39
      
 2: 20 + max  8 x1 + 16 x2 + 12 x4 +  6 x5 +  9 x6 +  2 x7
              3 x1 +  7 x2 +  6 x4 +  3 x5 +  5 x6 +  2 x7 ≤ 8
    sol:        1       5/7     0       0       0       0
    ub = 39

 3: 36 + max  0
              0 ≤ 1
    sol       
    ub = 36

 4: 20 + max  8 x1 + 12 x4 +  6 x5 +  9 x6 +  2 x7
              3 x1 +  6 x4 +  3 x5 +  5 x6 +  2 x7 ≤ 8
    sol:        1       5/6     0       0       0
    ub = 38

 5: 32 + max  2 x7
              2 x7 ≤ 2
    sol         1
    ub = 34

 6: 20 + max  8 x1 +  6 x5 +  9 x6 +  2 x7
              3 x1 +  3 x5 +  5 x6 +  2 x7 ≤ 8
    sol:        1       1       2/5     0
    ub = 37

 7: 29 + max  8 x1 +  6 x5 +  2 x7
              3 x1 +  3 x5 +  2 x7 ≤ 3
    sol:        1       0       0
    ub = 37, nouveau record z*=37

 8: 20 + max  8 x1 +  6 x5 +  2 x7
              3 x1 +  3 x5 +  2 x7 ≤ 8
    sol:        1       1       1
    ub = 36

 9:  0 + max  8 x1 + 16 x2 + 12 x4 +  6 x5 +  9 x6 +  2 x7
              3 x1 +  7 x2 +  6 x4 +  3 x5 +  5 x6 +  2 x7 ≤ 17
    sol:        1       1       1       1/3     0       0
    ub = 38

10:  6 + max  8 x1 + 16 x2 + 12 x4 +  9 x6 +  2 x7
              3 x1 +  7 x2 +  6 x4 +  5 x6 +  2 x7 ≤ 14
    sol:        1       1       2/3     0       0
    ub = 38

11: 18 + max  8 x1 + 16 x2 +  9 x6 +  2 x7
              3 x1 +  7 x2 +  5 x6 +  2 x7 ≤ 8
    sol:        1       5/7     0       0
    ub = 37

12: 6 + max  8 x1 + 16 x2 +  9 x6 +  2 x7
             3 x1 +  7 x2 +  5 x6 +  2 x7 ≤ 14
    sol:       1       1       4/5     0
    ub = 37
    
13:  0 + max  8 x1 + 16 x2 + 12 x4 +  9 x6 +  2 x7
              3 x1 +  7 x2 +  6 x4 +  5 x6 +  2 x7 ≤ 17
    sol:        1       1       1       1/5     0
    ub = 37

Algorithme parallèle

Une grande partie des applications parallèles sont écrites selon un schéma bipolaire, une partie des tâches effectue les calculs et l'autre partie gère l'exécution et en particulier la distribution des données. Ce schéma est connu sous le nom de Maître-Esclave. Nous allons utiliser ce schéma pour paralléliser l'algorithme branch and bound pour le problème de sac à dos.

Le rôle du maître

Le maître lit le problème à partir d'un fichier de format suivant

n
1 c1 a1
2 c2 a2
...
n cn an
b

Puis il trie les objets, trouve le record initial et renvoie les données aux esclaves. Il gère le pool des sous-problèmes, envoie du travail aux esclaves, diffuse les nouveaux records, etc.

Le rôle des esclaves

Le travail des esclaves peut se résumer par la boucle suivante

repeter
{  envoyer au maître une demande de travail
   si on reçoit un ordre de s'arrêter, stop
   traiter le problème reçu. Il y a trois possibilités :
      - soit on élimine le problème
      - soit on trouve un nouveau record et on le communique au maître
      - soit on décompose le problème en 2 sous-problèmes et on les envoie au maître
}

Points à préciser

Comment arrêter l'application proprement ? Même si le pool du maître est vide, un esclave peut être en train de traiter un problème qui produit 2 nouveaux sous-problèmes.
Comment diffuser le record ? Un bon record permet d'éliminer beaucoup de sous-problèmes. C'est pourquoi le nouveau record trouvé par un esclave doit être rapidement diffusé aux tous les esclaves (soit en passant par le maître, soit par diffusion directe).
Comment réduire les communications ?
- Il n'est pas nécessaire de communiquer les coefficients c_i et a_i pour chaque sous-problème. Il suffit de transmettre peu d'informations. Lesquelles ?
- au lieu d'envoyer les deux sous-problèmes au maître, l'esclave peut traiter directement l'un d'eux.

Mesures de performance

Une fois votre programme opérationnel, vous ferez une série de tests

en variant la taille des instances traitées
en utilisant un nombre de machines différent
en utilisant un nombre d'esclaves différent

Vous reporterez les résultats sous la forme d'un graphique (par exemple fait avec gnuplot).

On peut trouver ici un bon générateur d'instances. Pour la phase de développement / tests vous pouvez vous servir de ce fichier. La valeur objective optimale est 2400.

Extensions

L'ordre de traitement des sous-problèmes du pool peut avoir des conséquences importantes sur la performance de l'algorithme. Expérimenter des stratégies différentes (FIFO, LIFO, le meilleur d'abord, ...).
Proposer un schéma décentralisé où chaque tâche a son propre pool. En cas d'épuisement du pool la tâche prend une partie du pool d'une autre tâche.

Vous pouvez vous servir de ce code séquentiel comme point de départ.