home	accès étudiants

Complexité des algorithmes - approche pratique

Un problème

Nous allons analyser quelques algorithmes de résolution d'un problème avec applications dans le traitement de signaux.

Soit x une séquence (un tableau) de n nombres. Trouver la sous-séquence dont la somme d'éléments est maximale.

Remarque : Si tous les nombres sont négatifs on considère que la sous-séquence de somme maximale est vide et la somme maximale est 0.

Exemple : x = [31, -41, 59, 26, -53, 58, 97, -93, -23, 84]. La sous-séquence de somme maximale est [59, 26, -53, 58, 97] et cette somme est x[3...7] = 187.

Exercice 1

Proposer un algorithme de résolution de ce problème. Déterminer la complexité de cet algorithme.

Quatre algorithmes

Considérons les quatre algorithmes suivants :

Algorithme 1: Une approche directe consiste à parcourir toutes les sous-séquences. On calcule la somme d'éléments de chaque sous-séquence et compare avec la somme maximale trouvée jusqu'à maintenant. Autrement dit, pour chaque 1 ≤ l ≤ u ≤ n on calcule la somme x[l...u] = x[l] + ... + x[u].
Algorithme 2: Une méthode simple d'accélérer l'algorithme précédent est basée sur le fait que x[l...u] = x[l...u-1] + x[u]. On peut donc utiliser la somme x[l...u-1] calculée précédemment pour calculer la somme x[l...u].
Algorithme 3: C'est un algorithme basé sur le principe « diviser pour régner ». On divise la séquence en deux. On calcule la somme maximale dans chaque moitié et on trouve la sous-séquence de somme maximale qui contient le milieu. La solution est la maximale parmi ces trois sommes.
Algorithme 4: Supposons que le problème soit résolu pour x[1]...x[i-1]. La solution pour x[1]...x[i] est soit la solution précédente, soit la séquence de somme maximale qui se termine dans x[i].

J'ai implémenté les quatre algorithmes en Java. La classe MaxSubSum a un constructeur qui remplit le tableau avec des nombres aléatoires et des méthodes calc1() - calc4() qui correspondent aux algorithmes 1-4.

Exercice 2

Exécuter le programme et observer les résultats. Quel est le plus rapide parmi les quatre algorithmes ? Avec quelques modifications dans la méthode main et quelques exécutions déterminer la taille maximale des problèmes qui peuvent être résolu par algorithme 1 dans moins d'une minute. Idem pour algorithmes 2, 3, 4.

Performances

J'ai mesuré le temps d'exécution des quatre algorithmes sur un Intel® Pentium® 4 à 1.8GHz en variant la taille n des problèmes. Voici quelques plots du temps d'exécution en fonction de la taille du problème avec « zooms » différents.

Exercice 3

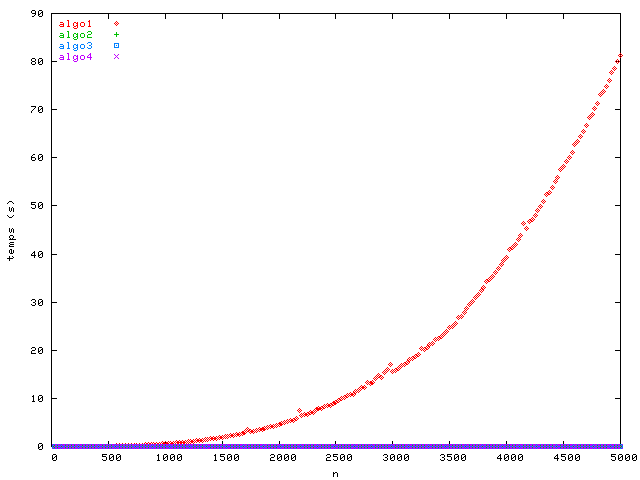
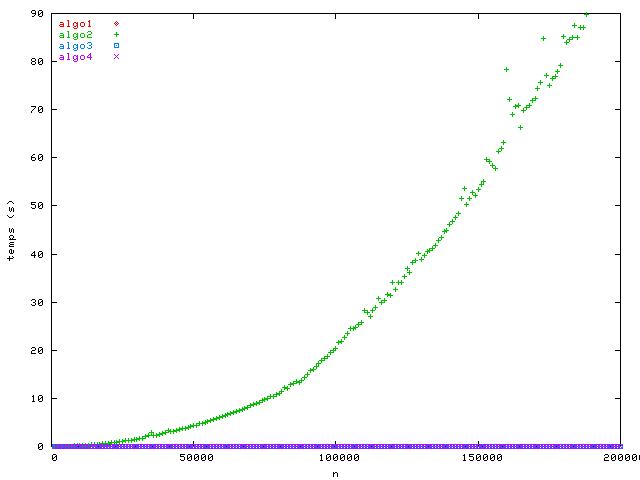
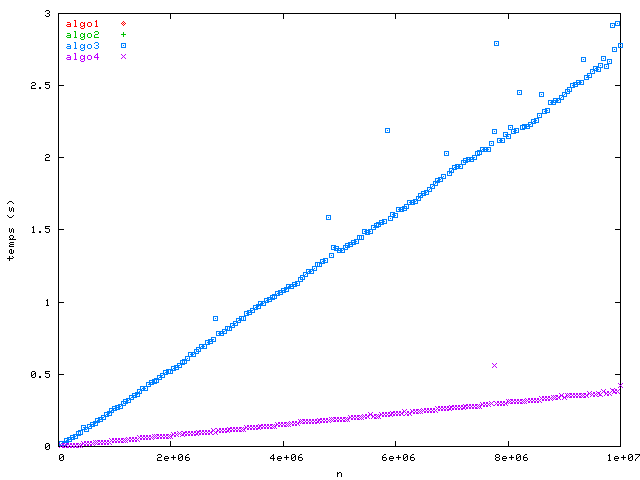
Déterminer la complexité de chacun des quatre algorithmes

Complexité et temps d'exécution

En titre d'exemple, considérons l'algorithme 2. Sa complexité est O(n²), ce qui signifie qu'il existe une constante k et un nombre N, tels que pour tout n ≥ N, le temps d'exécution t(n) est majoré par kn².

Même si ce n'est pas le « vrai » temps d'exécution, t(n)=cn² est une bonne approximation du temps d'exécution. Pour illustrer ça, j'ai comparé l'implémentation en Java et une implémentation en C de l'algorithme 2.

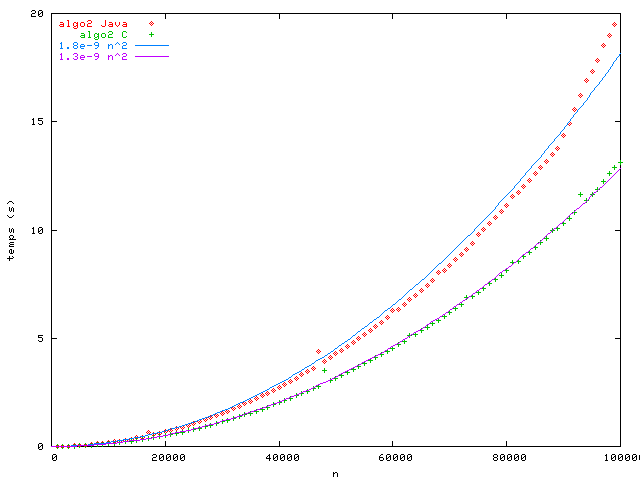
On voit que cn² est bien proche du temps d'exécution pour les deux implémentations. Les constantes c_JAVA=1.8e-9 et c_C=1.3e-9 sont déterminées à partir des données expérimentales par la méthode des moindres carrées itérative. Grosso modo, l'implémentation en C est 1.4 fois plus rapide que celle en Java. Néanmoins, le comportement de l'algorithme ne change pas. Il me suffit d'exécuter le programme en Java sur une machine à 2.5GHz pour obtenir la performance de l'implémentation en C sur ma machine, quelque soit la taille du problème.

Exercice 4

Soit t le temps d'exécution d'algorithme i, i=1,2,4 pour un problème de taille n.

Quel est le temps d'exécution pour un problème de taille 10 n ?
Quel est le temps d'exécution pour un problème de taille n sur une machine 10 fois plus rapide ?
Quelle est la taille maximale d'un problème qu'on peut résoudre sur une machine 10 fois plus rapide, ne dépassant pas le temps d'exécution t ?

L'ordre de grandeur et les constantes

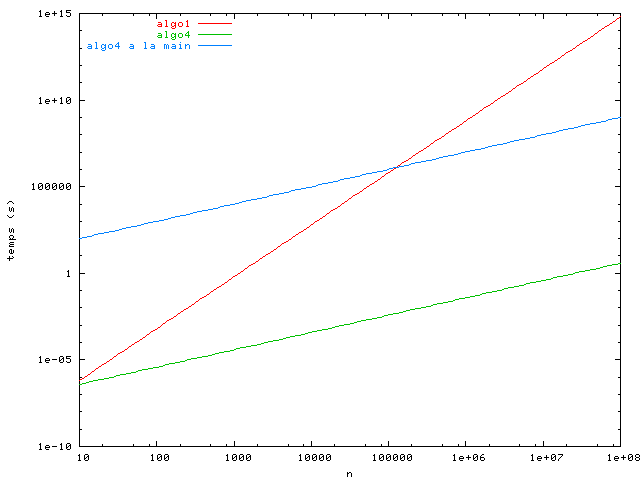
J'ai fait une estimation du temps d'exécution de chaque algorithme basée sur son ordre de complexité et les données expérimentales. Voici les résultats (la taille du problème et le temps d'exécution sont en échelle logarithmique). On voit que pour n < 1000 les quatre algorithmes prennent moins d'une seconde. Pour n = 1 000 000 algorithmes 3 et 4 sont toujours au dessous d'une seconde, tandis que l'algorithme 2 prend 1 heure et l'algorithme 1 prend environ un siècle !

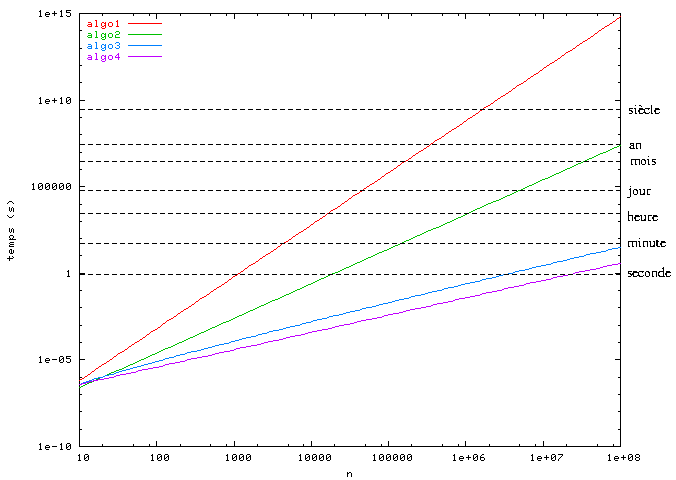
L'ordre de grandeur caractérise le comportement d'un algorithme. Les constantes dépendent de détails comme l'implémentation ou la machine cible. Un algorithme de plus faible complexité sera beaucoup plus rapide sur un problème de taille importante. Supposons que j'exécute algorithme 4 à la main en faisant une itération en 10 secondes. Pour n > 100 000 je serai plus rapide que mon ordinateur qui exécute l'algorithme 1 !